Gnaiger 2014 Abstract MiP2014
| Cell ergometry: OXPHOS and ET-pathway coupling efficiency. |
Link:
Mitochondr Physiol Network 19.13 - MiP2014
Gnaiger E (2014)
Event: MiP2014
Biochemical cell ergometry aims at measurement of JO2,max (compare VO2,max in exercise ergometry of humans and animals) of cell respiration linked to phosphorylation of ADP to ATP. The corresponding OXPHOS-capacity is based on saturating concentrations of ADP, [ADP]*, and inorganic phosphate, [Pi]*, available to the mitochondria. This is metabolically opposite to uncoupling respiration, which yields ET-capacity. The OXPHOS state can be established experimentally by selective permeabilization of cell membranes with maintenance of intact mitochondria, titrations of ADP and Pi to evaluate kinetically saturating conditions, and establishing fuel substrate combinations which reconstitute physiological TCA cycle function.
Labels: MiParea: Respiration
Coupling state: OXPHOS
HRR: Oxygraph-2k Event: A4, Oral MiP2014
Affiliation
1-Daniel Swarovski Research Lab, Mitochondrial Physiol, Dep Visceral, Transplant Thoracic Surgery, Medical Univ Innsbruck; 2-Oroboros Instruments, Innsbruck, Austria. - [email protected]
Abstract
Analogous to ergometric measurement of VO2max or VO2peak on a cycle or treadmill, cell ergometry is based on OXPHOS analysis to determine OXPHOS capacity, JO2P=P [pmol O2·s-1·mg-1], at the cellular and mitochondrial level. VO2peak and JO2P provide reference values for a subject’s or a cell’s aerobic or mitochondrial competence. Aerobic catabolic flux (1 ml O2·min-1·kg-1 = 0.744 µmol·s-1·kg-1) is multiplied by the corresponding Gibbs force (ΔkGO2=∂G/∂kξO2; typically -470 kJ/mol or -0.47 J/µmol O2) to obtain the mass-specific aerobic input power [W·kg-1]. The corresponding mechanical output power, Ppeak [W·kg-1], in cycle ergometry results in ergodynamic efficiencies [1] of about 0.25,
εpeak = Ppeak/-(JO2peak·ΔkGO2) = (Ppeak/JO2peak) / -ΔkGO2 (1)
In OXPHOS analysis the output power is mitochondrial ATP production, J~P=~P, times the Gibbs force of phosphorylation (ΔpG~P=∂G/∂pξ~P), which is typically 48 to 62 kJ/mol ~P [1]. Ergodynamic efficiency is a power ratio, partitioned into a flux ratio (the famous ~P/O2 ratio; ATP yield per oxygen consumed, Y~P/O2 = J~P/JO2P = ~P/P) and force ratio,
εP = (J~P·ΔpG~P)/-(JO2P·ΔkGO2) = ~P/P ∙ ΔpG~P/-ΔkGO2 = j≈P ∙ f≈P (2)
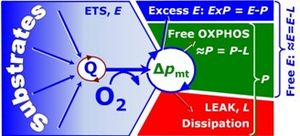
The upper limit of ~P/P is the mechanistic ~P:O2 ratio or stoichiometric number, ν~P/O2. The free respiratory OXPHOS capacity, ≈P=P-L, is potentially available to drive phosphorylation, ~P (Figure 1). Quantitatively justified in cases [3] but better adjusted to the protonmotive force, Δpmt, the dissipative LEAK component, L, in the OXPHOS state P can be assessed by respiration, L, measured in the LEAK state,
ν~P/O2 = ~Plimit/P = ~P/(P-L) = ~P/≈P (3)
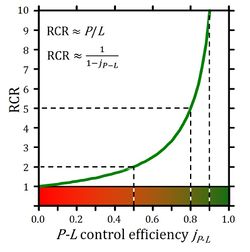
~P/P divided by ~P/≈P defines the OXPHOS coupling efficiency, j≈P, as a normalized flux ratio, which is a hyperbolic function of RCR (Figure 2) [5],
j≈P = ≈P/P = (P-L)/P = 1-L/P = 1-RCR-1 (4)
OXPHOS coupling efficiency in Equation (4) is determined by respirometric OXPHOS analysis. At the limit of maximum j≈P=1.0 the dissipative LEAK processes, L, are zero. Ergodynamic efficiency, ε, not only depends on mechanistic coupling but also on the force ratio or force efficiency. At ergodynamic equilibrium, ε=1.0, fluxes vanish to zero when j≈P = f≈P = 1 (Equation 2).
The OXPHOS state can be established experimentally in cells or tissues by selective permeabilization of plasma membranes, with ADP and Pi at kinetic saturation and fuel substrate combinations which reconstitute physiological TCA cycle function (Figure 1). The free OXPHOS capacity may be kinetically limited by the phosphorylation system to utilize Δpmt. Then ET-capacity is in excess of OXPHOS capacity by the factor jExP=(E-P)/E. Such kinetic limitation diminishes the effective j≈P independent of coupling control. Therefore, the ET-pathway coupling efficiency is defined as j≈E=(E-L)/E (compare Eq. 4) and related to j≈P by taking into account the apparent ET-pathway excess capacity (Figure 1),
j≈E = j≈P∙(1-jExP) + jExP (5)
Flux control factors and coupling efficiencies were derived from principles of thermodynamics rather than arbitrarily introduced as jargon of a specialized discipline.
Figures 1 and 2
Figure 1. Capacities for ET-pathway, OXPHOS and LEAK respiration (E, P, L). Free devided by total OXPHOS capacity, ≈P/P, is the OXPHOS coupling efficiency; free divided by total ET-capacity, ≈E/E, is the ET coupling efficiency [2]. The ET-pathway excess capacity, ExP, is available for coupled processes other than phosphorylation.
Figure 2. Respiratory acceptor control ratio as a function of OXPHOS coupling efficiency, jP-L. RCR is the State 3/State 4 flux ratio [4], equal to P/L if State 3 is at saturating [ADP] and [Pi]. RCR from 1.0 to infinity is highly non-linear in the typical experimental range of RCR 3 to 10: when j≈P increases from 0.8 to 0.9, RCR doubles from 5 to 10. RCR increases to infinity at the limit of jP-L=1.0. Statistical analyses of RCR±SD require linearization by transformation to jP-L.
References and acknowledgements
Supported by K-Regio project MitoCom Tyrol.
- Gnaiger E (1993) Efficiency and power strategies under hypoxia. Is low efficiency at high glycolytic ATP production a paradox? In: Surviving hypoxia: mechanisms of control and adaptation. Hochachka PW, Lutz PL, Sick T, Rosenthal M, Van den Thillart G (eds) CRC Press: 77-109. »Bioblast Access
- Gnaiger E (2014) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 4th ed. Mitochondr Physiol Network 19.12. Oroboros MiPNet Publications, Innsbruck. »Open Access
- Gnaiger E (2001) Bioenergetics at low oxygen: dependence of respiration and phosphorylation on oxygen and adenosine diphosphate supply. Respir Physiol 128: 277-97. »Bioblast Access
- Chance B, Williams GR (1955) Respiratory enzymes in oxidative phosphorylation: III. The steady state. J Biol Chem 217: 409-27. »Open Access
- Correction of printed version: In Eq.(4), L-P was written instead of the corrected P-L.
>> Cell ergometry
![]()
![]()
![]()
![]() -
-