Gnaiger 2015 Abstract MiPschool Cape Town 2015 II
| On coupling control of mitochondrial respiration. What is wrong with the RCR? |
Link:
Gnaiger E (2015)
Event: MiPschool Cape Town 2015
Electron transfer through respiratory enzyme complexes is partially coupled to the phosphorylation of ADP to ATP by intermediary generation and utilization of the mt-membrane potential, Δpmt. The electron transfer-pathway (ET-pathway) provides the driving input power with a chemical potential spanning from reduced electron donors (the fuel substrates) to the electron acceptor oxygen. At a theoretical maximum efficiency of 1.0, this input power would be fully backed off by a corresponding output power of proton translocation against a maximal output force Δpmt, when fluxes would be reduced to zero in a fully coupled system. Maximal efficiency in the ADP-stimulated state of oxidative phosphorylation (OXPHOS) is, however, not adaptive [1] and is not observed in mitochondria for two reasons: (i) For fluxes to proceed and work to be done, output forces must be moderately high in relation to input forces, such that Gibbs energy is partially dissipated (mainly as heat in aerobic metabolism) and partially conserved as biochemical exergy [2]. (ii) Non-mechanical, incompletely coupled systems dissipate part of the potential energy in short-circuits (LEAK). Biochemical coupling is determined by measurement of respiratory fluxes in rigorously defined coupling states at constant ET-competent substrate states.
![]() OXPHOS capacity, P, is the respiratory capacity of mitochondria at saturating concentrations of ADP, inorganic phosphate, oxygen, and defined CHO fuel substrates. Intrinsic uncoupling and dyscoupling lower the efficiency and contribute to the control of flux in the OXPHOS state. ADP and inorganic phosphate do not equilibrate across the plasma membrane, and saturating concentrations of these metabolites can hardly be achieved in living cells. Therefore, cell membranes are permeabilized while maintaining mitochondria intact for the study of OXPHOS capacity, which provides a model for biochemical cell ergometry [3].
OXPHOS capacity, P, is the respiratory capacity of mitochondria at saturating concentrations of ADP, inorganic phosphate, oxygen, and defined CHO fuel substrates. Intrinsic uncoupling and dyscoupling lower the efficiency and contribute to the control of flux in the OXPHOS state. ADP and inorganic phosphate do not equilibrate across the plasma membrane, and saturating concentrations of these metabolites can hardly be achieved in living cells. Therefore, cell membranes are permeabilized while maintaining mitochondria intact for the study of OXPHOS capacity, which provides a model for biochemical cell ergometry [3].
• O2k-Network Lab: AT Innsbruck Oroboros, AT Innsbruck Gnaiger E
Labels: MiParea: Respiration, mt-Membrane
Enzyme: Supercomplex
Coupling state: LEAK, ROUTINE, OXPHOS, ET Pathway: N, S, ROX
Abstract continued
![]() Respiration of intact cells is regulated according to physiological activity, at intracellular non-saturating ADP levels in ROUTINE states of activity. R increases under conditions of activation, and may be depressed with compensation by anaerobic metabolism, e.g. at high glucose concentration (Crabtree effect). ROUTINE activity including aerobic energy expenditure for cell growth is fundamentally different from the definition of basal metabolic rate (BMR).
Respiration of intact cells is regulated according to physiological activity, at intracellular non-saturating ADP levels in ROUTINE states of activity. R increases under conditions of activation, and may be depressed with compensation by anaerobic metabolism, e.g. at high glucose concentration (Crabtree effect). ROUTINE activity including aerobic energy expenditure for cell growth is fundamentally different from the definition of basal metabolic rate (BMR).
![]() ET capacity is measured in an open-circuit operation of the proton pumps. State E is induced by uncoupler titrations using protonophores (CCCP, FCCP, DNP) at optimum concentrations for stimulation of maximum oxygen flux (noncoupled state). Protonophores do not uncouple electron transfer from proton translocation, but dissipate energy of translocated protons as a bypass of ATP synthesis. Respiration is inhibited by high uncoupler concentrations. E exceeds the OXPHOS capacity in many cell types when P is limited by the capacity of the phosphorylation system. Therefore, E-R in general is not a respiratory reserve or spare capacity for phosphorylation.
ET capacity is measured in an open-circuit operation of the proton pumps. State E is induced by uncoupler titrations using protonophores (CCCP, FCCP, DNP) at optimum concentrations for stimulation of maximum oxygen flux (noncoupled state). Protonophores do not uncouple electron transfer from proton translocation, but dissipate energy of translocated protons as a bypass of ATP synthesis. Respiration is inhibited by high uncoupler concentrations. E exceeds the OXPHOS capacity in many cell types when P is limited by the capacity of the phosphorylation system. Therefore, E-R in general is not a respiratory reserve or spare capacity for phosphorylation.
![]() LEAK respiration compensates for proton leak, slip (protons not finally translocated across the mt-membrane) and cation cycling (Ca2+, K+). L is influenced to a small extent by electron leak linked to ROS production. LEAK or L is, therefore, an acronym beyond the proton leak. L is measured as mitochondrial respiration in the presence of fuel substrate(s) and absence of ADP (a: no adenylates, LN; b: ATP only, LT), or (c) after inhibition of the phosphorylation system, LOmy. At a given proton leak, L depends inversely on the H+/O2 ratio and is thus lower for CI-linked (three coupling sites) compared to CII-linked electron flow (two coupling sites). The high Δpmt exerts feedback control by depressing oxygen flux.
LEAK respiration compensates for proton leak, slip (protons not finally translocated across the mt-membrane) and cation cycling (Ca2+, K+). L is influenced to a small extent by electron leak linked to ROS production. LEAK or L is, therefore, an acronym beyond the proton leak. L is measured as mitochondrial respiration in the presence of fuel substrate(s) and absence of ADP (a: no adenylates, LN; b: ATP only, LT), or (c) after inhibition of the phosphorylation system, LOmy. At a given proton leak, L depends inversely on the H+/O2 ratio and is thus lower for CI-linked (three coupling sites) compared to CII-linked electron flow (two coupling sites). The high Δpmt exerts feedback control by depressing oxygen flux.
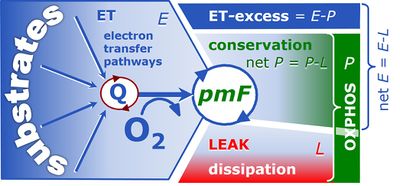
Figure. 1. Respiratory states (ET, OXPHOS and LEAK) and corresponding respiration (E, P, L). Free divided by total OXPHOS capacity, ≈P/P, is the OXPHOS coupling efficiency; free divided by total ET capacity, ≈E/E, is the ET-coupling efficiency. The ET-excess capacity, ExP, is available for processes other than phosphorylation [3].
![]() The free OXPHOS capacity, ≈P, is the OXPHOS capacity corrected for LEAK respiration. ≈P=P-L is the respiratory capacity potentially available for phosphorylation of ADP to ATP. Oxygen consumption in the OXPHOS state, therefore, is partitioned into the free OXPHOS capacity, ≈P, strictly coupled to phosphorylation, P», and nonphosphorylating LEAK respiration, LP: P = ≈P+LP. It is frequently assumed that L as measured in the LEAK state overestimates the LEAK component of respiration, LP, as measured in the OXPHOS state, particularly if Δpmt is not adjusted to equivalent levels in states L and P. However, if the LEAK component increases with enzyme turnover during P, the low enzyme turnover during L may counteract the effect of the higher Δpmt [4].
The free OXPHOS capacity, ≈P, is the OXPHOS capacity corrected for LEAK respiration. ≈P=P-L is the respiratory capacity potentially available for phosphorylation of ADP to ATP. Oxygen consumption in the OXPHOS state, therefore, is partitioned into the free OXPHOS capacity, ≈P, strictly coupled to phosphorylation, P», and nonphosphorylating LEAK respiration, LP: P = ≈P+LP. It is frequently assumed that L as measured in the LEAK state overestimates the LEAK component of respiration, LP, as measured in the OXPHOS state, particularly if Δpmt is not adjusted to equivalent levels in states L and P. However, if the LEAK component increases with enzyme turnover during P, the low enzyme turnover during L may counteract the effect of the higher Δpmt [4].
![]() Dissipative LEAK respiration restricts the extent to which E is available to drive coupled transmembrane processes. The remaining free ET capacity, ≈E=E-L, is partitioned into the free OXPHOS module, ≈P, and the excess capacity module, ExP (Fig. 1).
Dissipative LEAK respiration restricts the extent to which E is available to drive coupled transmembrane processes. The remaining free ET capacity, ≈E=E-L, is partitioned into the free OXPHOS module, ≈P, and the excess capacity module, ExP (Fig. 1).
![]() Measurement of the ET-excess capacity, ExP=E-P, provides a tool for the diagnosis of a specific impairment of the phosphorylation system in toxicological or pathological states. ExP increases if OXPHOS is diminished relative to ET capacity, which leads to the unequivocal distinction between defects of the electron transfer versus phorphorylation system. Both can potentially limit ≈P, the vital free OXPHOS capacity [5].
Measurement of the ET-excess capacity, ExP=E-P, provides a tool for the diagnosis of a specific impairment of the phosphorylation system in toxicological or pathological states. ExP increases if OXPHOS is diminished relative to ET capacity, which leads to the unequivocal distinction between defects of the electron transfer versus phorphorylation system. Both can potentially limit ≈P, the vital free OXPHOS capacity [5].
The P»/O2 ratio is a biochemical expression of efficiency measured as the stoichiometric yield of ATP (P») per consumed O2 (4 e) or O (2 e). The P»/O2 ratio depends on the coupling state of mitochondria. P»/O2 is zero at opposite limits of (i) maximal noncoupled respiration at low Δpmt in State E, (ii) minimum respiration at maximum Δpmt in State L, and (iii) at full inhibition of electron transfer when O2 flux is limited to residual oxygen consumption (ROX). ROX is subtracted from total oxygen flux in the various coupling states. Flux ratios derived from different coupling states represent the most easily accessible indices of biochemical coupling efficiency.
Analogous to ergometric measurement of VO2max or VO2peak on a cycle or treadmill, cell ergometry is based on OXPHOS analysis to determine OXPHOS capacity, JO2P=P [pmol O2•s-1•mg-1], at the cellular and mitochondrial level. VO2peak and JO2P provide reference values for a subject’s or a cell’s aerobic fitness. Aerobic catabolic flux (1 ml O2•min-1•kg-1 = 0.744 µmol•s-1•kg-1) is multiplied by the corresponding Gibbs force (ΔkGO2=∂G/∂kζO2; typically -470 kJ/mol or -0.47 J/µmol O2) to obtain the mass-specific aerobic input power [W•kg-1]. The corresponding mechanical output power, Ppeak [W•kg-1], in cycle ergometry results in ergodynamic efficiencies [1,2] of about 0.25,
εpeak = Ppeak/-(JO2peak•ΔkGO2) = (Ppeak/JO2peak) / -ΔkGO2 (Eq. 1)
In OXPHOS analysis the output power is mitochondrial ATP production, JP»=P», times the Gibbs force of phosphorylation (ΔpGP»=∂G/∂pζP»), which is typically 48 to 62 kJ/mol P» [1]. Ergodynamic efficiency is a power ratio, partitioned into the P»/O2 flux ratio (YP»/O2 = JP»/JO2P = P»/P) and force ratio,
εP = (JP»•ΔpGP»)/-(JO2P•ΔkGO2) = P»/P • ΔpGO2) = j≈P • f≈P (Eq. 2)
The upper limit of P»/P is the mechanistic P»:O2 ratio or stoichiometric number, νP»/O2,
νP»/O2 = P»limit/P = P»/(P-L) = P»/≈P (Eq. 3)
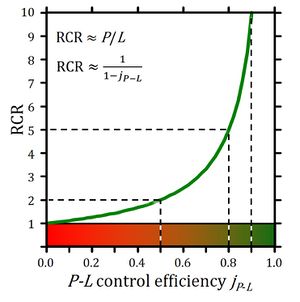
The free respiratory OXPHOS capacity, ≈P=P-L, is potentially available to drive phosphorylation, P» (Fig. 1). P»/P divided by P»/≈P defines the OXPHOS coupling efficiency, j≈P, as a normalized flux ratio, which is a hyperbolic function of RCR (Fig. 2),
j≈P = ≈P/P = (L-P)/P = 1-L/P = 1-RCR-1 (Eq. 4)
Figure 2. Respiratory acceptor control ratio as a function of OXPHOS coupling efficiency, j≈P. RCR is the State 3/State 4 flux ratio [6], equal to P/L if State 3 is at saturating [ADP] and [Pi]. RCR from 1.0 to infinity is highly non-linear in the typical experimental range of RCR 3 to 10: when j≈P increases from 0.8 to 0.9, RCR doubles from 5 to 10. RCR increases to infinity at the limit of j≈P=1.0. Statistical analyses of RCR±SD require linearization by transformation to j≈P [3].
OXPHOS coupling efficiency (Eq. 4) is determined by respirometric OXPHOS analysis. At the limit of maximum j≈P=1.0 the dissipative LEAK processes, L, are zero. Ergodynamic efficiency, ε, not only depends on coupling but also on the force ratio or force efficiency. At ergodynamic equilibrium, ε=1.0, fluxes vanish to zero when j≈P = f≈P = 1 (Eq. 2).
The OXPHOS state can be established experimentally in cells or tissues by selective permeabilization of plasma membranes, with ADP and Pi at kinetic saturation and fuel substrate combinations which reconstitute physiological TCA cycle function (Fig. 1). The free OXPHOS capacity may be kinetically limited by the phosphorylation system to utilize Δpmt. Then ET capacity is in excess of OXPHOS capacity by the factor jExP=(E-P)/E. Such kinetic limitation diminishes the effective j≈P independent of coupling control. Therefore, the ET-coupling efficiency is defined as j≈E=(E-L)/E (compare Eq. 4) and related to j≈P by taking into account the apparent ET-excess capacity (Fig. 1),
j≈E = j≈P•(1-jExP) + jExP (Eq. 5)
Flux control factors [3] and coupling efficiencies are derived from principles of thermodynamics rather than arbitrarily introduced as jargon of a specialized discipline [7].
Affiliation
- Swarovski Research Lab, Dept Visceral, Transplant Thoracic Surgery, Medical Univ Innsbruck;
- Oroboros Instruments, Innsbruck, Austria. - [email protected]
References and acknowledgements
- Gnaiger E (1993) Efficiency and power strategies under hypoxia. Is low efficiency at high glycolytic ATP production a paradox? In: Surviving Hypoxia: Mechanisms of Control and Adaptation. Hochachka PW, Lutz PL, Sick T, Rosenthal M, Van den Thillart G (eds) CRC Press, Boca Raton, Ann Arbor, London, Tokyo:77-109. »Bioblast Access«
- Gnaiger E (1993) Nonequilibrium thermodynamics of energy transformations. Pure Appl Chem 65:1983-2002.
- Gnaiger E (2014) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 4th ed. Mitochondr Physiol Network 19.12. Oroboros MiPNet Publications, Innsbruck:80 pp.
- Garlid KD, Semrad C, Zinchenko V (1993) Does redox slip contribute significantly to mitochondrial respiration? In: Schuster S, Rigoulet M, Ouhabi R, Mazat J-P (eds) Modern trends in biothermokinetics. Plenum Press, New York, London:287-93.
- Lemieux H, Semsroth S, Antretter H, Hoefer D, Gnaiger E (2011) Mitochondrial respiratory control and early defects of oxidative phosphorylation in the failing human heart. Int J Biochem Cell Biol 43:1729–38.
- Chance B, Williams GR (1955) Respiratory enzymes in oxidative phosphorylation: III. The steady state. J Biol Chem 217:409-27.
- For more details visit: MitoPedia: Respiratory control ratios