Description
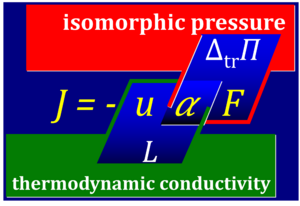
Linear phenomenological laws are at the core of the thermodynamics of irreversible processes TIP, considered to apply near equilibrium but more generally in transport processes (e.g. Fick's law). In TIP, linearity is discussed as the dependence of generalized flows I or fluxes J on generalized forces, J = -L·F, where L is expected to be constant (as a prerequisite for linearity) and must not be a function of the force F (affinity) for Onsager reciprocity to apply. This paradigm is challenged by the ergodynamic concept of fundamentally non-linear isomorphic flux-force relations and is replaced by the generalized isomorphic flux-pressure relations. Flows I [MU·s-1] and forces F [J·MU-1] are conjugated pairs, the product of which yields power, I·F = P [J·s-1 = W]. Flux J is system-size specific flow, such that volume-specific flux times force yields volume-specific power, PV = J·F [W·m-3]. Then vectoral and vectorial transport processes are inherently non-linear flux-force relationships, with L = u·c in continuous transport processes along a gradient (c is the local concentration), or L = u·α (α is the free activity in a discontinuous transport process across a semipermeable membrane) — formally not different from (isomorphic to) scalar chemical reactions.
Reference: Gnaiger 2020 BEC MitoPathways, Gnaiger 1989 Energy Transformations, MitoPedia: Ergodynamics
Communicated by Gnaiger Erich 2022-10-24
Linear laws in transport processes are not linear flux-force laws
- In TIP, the linearity between 'generalized flux' and 'generalized force' is emphasized to apply to transport processes:
- 'In contrast to the simple behavior of transport processes, the linear relations between rates and affinities are not always sufficient and in many cases it is necessary to take into account non-linear relations like (5.14).' - (p. 59 in Prigogine 1967 Interscience)
- 'Even in the validity range of the Gibbs formula the relations between chemical rates and affinities may be non-linear (see, i.e., (5.14)). This is in contrast with transport processes where we restrict ourselves to linear laws with respect to the forces. - (p. 94 in Prigogine 1967 Interscience)
Flux-force problems and flux-pressure solutions
- Generalized fluxes (p. 40 in Prigogine 1967 Interscience) must be distinguished from flows. The term 'rate' is ambiguous.
- An amazingly vague terminology is used in physical chemistry, where 'natural assumptions' are not expected, since such assumptions can be easily replaced by rigorous isomorphic analyses and are falsified by such anayses. 'It is quite natural to assume, at least close to equilibrium, that we have linear relations between the rates and the affinities. Such a scheme automatically includes empirical laws as Fourier's law for heat flow or Fick's law for diffusion.' - (p. 44/45 in Prigogine 1967 Interscience)
- From J = L·X in TIP, it follows that affinities X are generalized forces, X = -F.
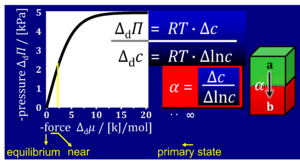
- Fick's law for diffusion is a linear law of the form I = -u·ΔΠ for discontinuous transport across a semipermeable membrane. I [mol·s-1] times Π [Pa = J·m-3] does not yield power P [W = J·s-1]. Fick's law, therefore, must not be considered as a linear phenomenological flow-force law, but instead a linear flow-pressure law, where the diffusion coefficient is D = u·RT and Π = RT·Δc. This yields the more familiar form of Fick's law as I = -D·Δc = -u·RT·Δc. The free activity α is pressure divided by force, i.e. pressure Π = RT·Δc [J·m-3] divided by force F = RT·Δlnc [J·mol-1]. Then α = Δc/Δlnc [mol·m-3]. From Fick's law in the form I = -u·α·F it can be seen that the phenomenological coefficient (thermodynamic conductivity L) combines the term mobility u related to the molecular details (particle size, membrane permeability) and free activity α, L = u·α. Then correctly P = I·F. In contrast, the ergodynamic pressure concept combines the free activity α and the force F which are interdependent, Π = α·F.
- The equation for the free activity α has been introduced in the context of the Kedem-Katchalsy equations with the quite misleading term 'logarithmic mean concentration' (Kedem 1958 Biochim Biophys Acta; Caplan 1983 Harvard Univ Press; Demirel 2004 J Phys Chem B). By restricting the view in TIP on (1) conditions when the phenomenological coefficient L is fairly constant and (2) linear relations between volume-flow and pressure, the fundamental flux-pressure relation escaped attention (Gnaiger 1989 Energy Transformations; Gnaiger 1992 Funct Ecol; Gnaiger 1993 Hypoxia), despite the fundamental treatment in Einstein's diffusion equation. Volume-flow times pressure is actually a unique flow-force relation, the concept of which goes back to Maxwell (1867). In contrast, the linear relation between flux of a diffusing amount of substance and pressure is not a flux-force relation.
- When flow I (extensive quantity) is normalized to obtain flux J (size-specific quantity), then a flux-force relation is obtained by application of the same normalization to I and L in I = -L·F. A flux-pressure relation is obtained by application of the same normalization to I and u.
- Concentrations c should be replaced by activities in the definition of chemical potentials and free activity α. It should be noted that many methods do not report concentrations but activities in the first place (e.g. electrochemical sensors such as the polarographic oxygen sensor or the glass pH electrode).
- Symbols (F, Π, L) are simplified here in a 'short-hand' style which may entail ambiguity and is avoided by using iconic symbols.
References
- Caplan SR, Essig A (1983) Bioenergetics and linear nonequilibrium thermodynamics. The steady state. Harvard Univ Press, Cambridge:435 pp. - »Bioblast link«
- Demirel Y, Sandler SI (2004) Nonequilibrium thermodynamics in engineering and science. J Phys Chem B 108:31-43. - »Bioblast link«
- Einstein A (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann Physik 4, XVII:549-60. - »Bioblast link«
- Fick A (1855) Über Diffusion. Pogg Ann 94:59-86. - »Bioblast link«
- Gnaiger E (1987) Optimum efficiencies of energy transformation in anoxic metabolism. The strategies of power and economy. In: Calow P (ed) Evolutionary physiological ecology. Cambridge Univ Press:7-36. - »Bioblast link«
- Gnaiger E (1989) Mitochondrial respiratory control: energetics, kinetics and efficiency. In: Wieser W, Gnaiger E (eds) Energy transformations in cells and organisms. Thieme, Stuttgart:6-17. - »Bioblast link«
- Gnaiger E (1992) Optimum efficiency of energy transformation and the evolution of catabolic pathways. Funct Ecol 6:234-41. - »Bioblast link«
- Gnaiger E (1993) Efficiency and power strategies under hypoxia. Is low efficiency at high glycolytic ATP production a paradox? In: Surviving hypoxia: Mechanisms of control and adaptation. Hochachka PW, Lutz PL, Sick T, Rosenthal M, Van den Thillart G (eds) CRC Press, Boca Raton, Ann Arbor, London, Tokyo:77-109. - »Bioblast link«
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002
- Kedem O, Katchalsky A (1958) Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim Biophys Acta 27:229-46. - »Bioblast link«
- Onsager L (1931) Reciprocal relations in irreversible processes. I. Phys Rev 37:405-26. »Bioblast link«
- Prigogine I (1967) Introduction to thermodynamics of irreversible processes. Interscience New York, 3rd ed:147pp. - »Bioblast link«
MitoPedia concepts:
Ergodynamics