Description
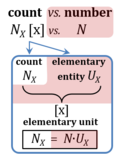
Count NX is the number N of elementary entities of entity-type X. The single elementary entity UX is a countable object or event. NX is the number of objects of type X, whereas the term 'entity' and symbol X are frequently used and understood in dual-message code indicating both (1) the entity-type X and (2) a count of NX = 1 x for a single elementary entity UX. 'Count' is synonymous with 'number of entities' (number of particles such as molecules, or objects such as cells). Count is one of the most fundamental quantities in all areas of physics to biology, sociology, economy and philosophy, including all perspectives of the statics of countable objects to the dynamics of countable events. The term 'number of entities' can be used in short for 'number of elementary entities', since only elementary entities can be counted, and as long as it is clear from the context, that it is not the number of different entity types that are the object of the count.
Abbreviation: NX [x]
Reference: Gnaiger MitoFit Preprints 2020.4, BEC2020.1, Gnaiger 2020 BEC MitoPathways
Communicated by Gnaiger Erich (2019-08-15) last update 2020-07-23 in: Anastrophe XX Entity X and elementary unit x of A X-mass Carol
Number, count, and recount
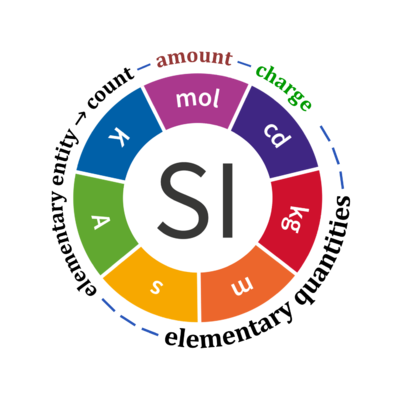
- In the International System of Units (SI), the quantity 'count' is explicitly considered as an exception: "Each of the seven base quantities used in the SI is regarded as having its own dimension. .. All other quantities, with the exception of counts, are derived quantities" (Bureau International des Poids et Mesures 2019 The International System of Units (SI)). Count is not included in the SI as a base quantity. Since 2019-05-20, the amount of substance, n, of a system is defined as "a measure of the number of specified elementary entities. An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles" (Bureau International des Poids et Mesures 2019). The quantity 'amount', n, therefore, is a number of specified elementary entities expressed in the unit 'mole' [mol] with dimension N. Logically, the quantities 'amount' and 'count' have exactly identical meanings, since the quantity 'count' NX is a number of specified elementary entities expressed in the unit 'elementary unit' [x] with dimension X. Similarly, charge is a derived SI unit with dimension A·T, converting the elementary unit [x] into coulombs [C] using the elementary charge.
- 'Count' NX (number of entities UX) and 'number' N are distinguished (German: Anzahl versus Zahl). A count is a quantity represented by a number N and the corresponding entity-type X (cell count: Nce). In contrast, a number is represented by numerals only, is a mathematical object used for counting, and is thus not a physicochemical quantity. Neither is a defined elementary entity-type X a count, it is rather the dimension of a count (entity type: cell, ce). Not all sample types contain countable objects. Countable objects are physicochemical particles (atoms, electrons, ions, molecules), ensembles (packaging units, parcels), biological entities (cells, organisms, individuals, patients), and units of transmitted information. The magnitude of a count is expressed by a number times the elementary unit [x]. The name 'elementary unit' is proposed for the unit [x]. x ('times') indicates in dynamics how many times a defined event is 're-counted' during a defined period of time, and in statics how many times different members of the defined entity-type are accounted for in a defined system. It is important not to mix statics with dynamics; the count of statics counts different members of the defined entity in the system, but does not re-count the same member of the defined entity in the system (consider the political problem of counting votes).
- Counts per volume of a mixture is a concentration [x·m-3] or [x·L-1]. Counts per area is an elementary area-density [x·m-2]. In dynamics, counts per time is a frequency, NX·t-1 [x·s-1]. Converting the time t travelled into distance l, counts per length can be considered as a distance-frequency NX·l-1 [x·m-1]. Compare the dynamic question on how many steps you take per second when you walk or run, with the static question on how many steps you take per 1 km distance covered. This expression in normal form is generally understandable, as expressed in canonical form: How many numbers Nstep of entities of entity-type 'steps' do you count per second when you walk or run? How many numbers Nsteps of entities of entity-type steps do you count per km when you move a distance of on km?
- SI prefixes are used with SI units, such as [kg], [µmol], [nm], [MHz]. Prefixes cannot be used with numbers. However, prefixes can be used with the elementary unit [x], applying the same convention for any symbol of SI units: Mx = 106 x; MHz = Mx·s-1; µx = 10-6 x; Gx = 109 x; nx = 10-9 x. If appropriate, it is convenient in statics to write simply 'unit' instead of 'elementary unit', and in dynamics to use 'times' instead of 'elementary unit'. Examples: Avogadro constant NA, expressed in 'elementary units per mole' [x·mol-1]; elementary charge e, expressed in 'coulombs per elementary unit' [C·x-1]; body mass is mass per single elementary body (not mass of several bodies) expressed in 'kilograms per unit' [kg·x-1]; frequency (counts per time, NX/t), expressed in 'units per second' (times per second) [x·s-1].
Base quantities and count
Quantity Symbol for quantity Q Symbol for dimension Name of abstract unit uQ Symbol for unit uQ [*] elementary entity *,$ UX U elementary unit x count *,$ NX = N·UX X elementary unit x amount of substance *,§ nX = NX·NA-1 N mole mol charge *,€ Qel = zX·e·NX I·T coulomb C = A·s length l L meter m mass m M kilogram kg time t T second s electric current I I ampere A thermodynamic temperature T Θ kelvin K luminous intensity Iv J candela cd
- [*] SI units, except for the canonical 'elementary unit' [x]. The following footnotes are canonical comments, related to iconic symbols.
- * For the elementary quantities NX, nX, and Qel, the entity-type X of the elementary entity UX has to be specified in the text and indicated by a subscript: nO2; Nce; Qel.
- $ Count NX equals the number of elementary entities UX. In the SI, the quantity 'count' is explicitly considered as an exception: "Each of the seven base quantities used in the SI is regarded as having its own dimension. .. All other quantities, with the exception of counts, are derived quantities" (Bureau International des Poids et Mesures 2019 The International System of Units (SI)). An elementary entity UX is a material unit, it is not a count (UX is not a number of UX). NX has the dimension X of a count and UX has the dimension U of an elementary entity; both quantities have the same abstract unit, the 'elementary unit' [x].
- § Amount nX is an elementary quantity, converting the elementary unit [x] into the SI base unit mole [mol] using the Avogadro constant NA.
- € Charge is a derived SI quantity. Charge is an elementary quantity, converting the elementary unit [x] into coulombs [C] using the elementary charge e, or converting moles [mol] into coulombs [C] using the Faraday constant F. zX is the charge number per elementary entity UX, which is a constant for any defined elementary entity UX. Qel = zX·F·nX
SI and IUPAC
- Unfortunately, the elementary unit [x] is not explicitly considered by the SI and IUPAC (Mohr and Philipps 2015). This causes confusion since then, for example, the unit 'joule' [J] relates without discrimination to both: (1) exergy per elementary entity, and (2) exergy of the system (instrumental chamber) or the (sub)sample in the system. In contrast, joule per elementary unit [J∙x-1] clearly indicates exergy per elementary entity. The unit [x] is a motive unit.
Stating quantity values being pure numbers (p. 151)
Bureau International des Poids et Mesures (2019) The International System of Units (SI). 9th edition:117-216 ISBN 978-92-822-2272-0. - »Open Access pdf«
- There are also some quantities that cannot be described in terms of the seven base quantities of the SI, but have the nature of a count. Examples are a number of molecules, a number of cellular or biomolecular entities (for example copies of a particular nucleic acid sequence), or degeneracy in quantum mechanics. Counting quantities are also quantities with the associated unit one. The unit one is the neutral element of any system of units – necessary and present automatically. There is no requirement to introduce it formally by decision. Therefore, a formal traceability to the SI can be established through appropriate, validated measurement procedures (Section 2.3.3, p. 136).
- As discussed in Section 2.3.3, values of quantities with unit one, are expressed simply as numbers. The unit symbol 1 or unit name “one” are not explicitly shown. SI prefix symbols can neither be attached to the symbol 1 nor to the name “one”, therefore powers of 10 are used to express particularly large or small values.
- Quantities that are ratios of quantities of the same kind (for example length ratios and amount fractions) have the option of being expressed with units (m/m, mol/mol) to aid the understanding of the quantity being expressed and also allow the use of SI prefixes, if this is desirable (μm/m, nmol/mol). Quantities relating to counting do not have this option, they are just numbers.
- The internationally recognized symbol % (percent) may be used with the SI. When it is used, a space separates the number and the symbol %. The symbol % should be used rather than the name “percent”. In written text, however, the symbol % generally takes the meaning of “parts per hundred”. Phrases such as “percentage by mass”, “percentage by volume”, or “percentage by amount of substance” shall not be used; the extra information on the quantity should instead be conveyed in the description and symbol for the quantity.
- The term “ppm”, meaning 10-6 relative value, or 1 part in 106, or parts per million, is also used. This is analogous to the meaning of percent as parts per hundred. The terms “parts per billion” and “parts per trillion” and their respective abbreviations “ppb” and “ppt”, are also used, but their meanings are language dependent. For this reason the abbreviations ppb and ppt should be avoided.
References
| Bioblast link | Reference | Year |
|---|---|---|
| Baroody 1983 J Research in Mathematics Education | Baroody AJ, Price J (1983) The development of number–word sequence in the counting of three-year-olds. J Research in Mathematics Education 14:361-8. | 1983 |
| Brown 2018 Metrologia | Brown RJC (2018) The evolution of chemical metrology: distinguishing between amount of substance and counting quantities, now and in the future. Metrologia 55:L25. https://doi.org/10.1088/1681-7575/aaace8 | 2018 |
| Brown 2021 Metrologia | Brown RJC (2021) A metrological approach to quantities that are counted and the unit one. Metrologia 58:035014. https://doi.org/10.1088/1681-7575/abf7a4 | 2021 |
| Bureau International des Poids et Mesures 2019 The International System of Units (SI) | Bureau International des Poids et Mesures (2019) The International System of Units (SI). 9th edition:117-216. ISBN 978-92-822-2272-0 | 2019 |
| Cohen 2008 IUPAC Green Book | Cohen ER, Cvitas T, Frey JG, Holmström B, Kuchitsu K, Marquardt R, Mills I, Pavese F, Quack M, Stohner J, Strauss HL, Takami M, Thor HL (2008) Quantities, Units and Symbols in Physical Chemistry. IUPAC Green Book 3rd Edition, 2nd Printing, IUPAC & RSC Publishing, Cambridge. | 2008 |
| Cooper 2012 Synthese | Cooper G, Humphry SM (2012) The ontological distinction between units and entities. Synthese 187:393–401. https://doi.org/10.1007/s11229-010-9832-1 | 2012 |
| Gnaiger 2020 BEC MitoPathways | Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002 | 2020 |
| Gnaiger 2020 MitoFit x | Gnaiger E (2021) The elementary unit — canonical reviewer's comments on: Bureau International des Poids et Mesures (2019) The International System of Units (SI) 9th ed. https://doi.org/10.26124/mitofit:200004.v2 | 2021 |
| BEC 2020.1 doi10.26124bec2020-0001.v1 | Gnaiger E et al ― MitoEAGLE Task Group (2020) Mitochondrial physiology. Bioenerg Commun 2020.1. https://doi.org/10.26124/bec:2020-0001.v1 | 2020 |
| Mohr 2015 Metrologia | Mohr Peter J, Phillips William D (2015) Dimensionless units in the SI. Metrologia 52:40-7. https://doi.org/10.1088/0026-1394/52/1/40 | 2015 |
- Bioblast links: SI base units - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Entity, count, and number, and SI base quantities / SI base units
Quantity name Symbol Unit name Symbol Comment elementary UX elementary unit [x] UX, UB; [x] not in SI count NX elementary unit [x] NX, NB; [x] not in SI number N - dimensionless = NX·UX-1 amount of substance nB mole [mol] nX, nB electric current I ampere [A] A = C·s-1 time t second [s] length l meter [m] SI: metre mass m kilogram [kg] thermodynamic temperature T kelvin [K] luminous intensity IV candela [cd]
- Fundamental relationships
- » Avogadro constant NA
- » Boltzmann constant k
- » elementary charge e
- » Faraday constant F
- » gas constant R
- » electrochemical constant f
- Fundamental relationships
- SI and related concepts
- Bioblast links: Normalization - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Quantities for normalization
- » Count in contrast to Number
- » Mitochondrial marker
- » O2k-Protocols: mitochondrial and marker-enzymes
- » Citrate synthase activity
- Quantities for normalization
- General
- Related keyword lists
MitoPedia concepts:
Ergodynamics